


Siguiente: 5.1.1 Radical neutro hidroximetilo
Subir: 5 Espectros de radicales
Anterior: 5 Espectros de radicales
Índice General
5.1 Radicales que contienen n núcleos equivalentes con I = 1/2
El diagrama de energía y espectro de RSE de un radical que contiene un núcleo con
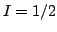 y un electrón se muestra en la Fig. 2.
y un electrón se muestra en la Fig. 2.
Los dos campos de resonancia se deducen de Ec. (5):
Figura 2:
Niveles de energía de un radical con un núcleo con I = 1/2 y espectro de RSE.
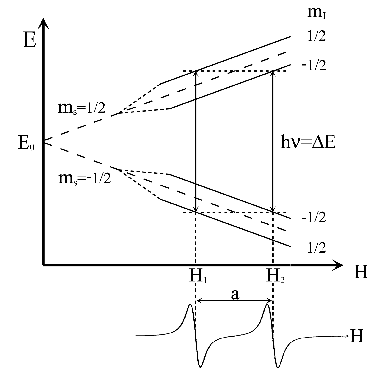 |
El espectro consta de dos líneas de igual intensidad (1:1); es decir un doblete;
la separación entre las dos líneas del doblete es el acoplamiento hiperfino 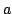 .
En la parte inferior de la Fig. 2 se ha representado la primera derivada
de la curva de absorción como es usual en Espectroscopia de RSE.
.
En la parte inferior de la Fig. 2 se ha representado la primera derivada
de la curva de absorción como es usual en Espectroscopia de RSE.
Si un radical contiene 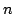 núcleos equivalentes (con idéntico entorno químico)
de espín
núcleos equivalentes (con idéntico entorno químico)
de espín  ocasionarán el mismo desdoblamiento hiperfino (igual valor de
ocasionarán el mismo desdoblamiento hiperfino (igual valor de 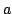 );
su espectro de RSE estará formado por
);
su espectro de RSE estará formado por 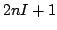 líneas equidistantes a los campos de resonancia:
líneas equidistantes a los campos de resonancia:
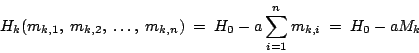 |
(6) |
donde 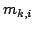 son los números cuánticos correspondientes a las componentes Z del momento angular de
espín nuclear de cada núcleo
son los números cuánticos correspondientes a las componentes Z del momento angular de
espín nuclear de cada núcleo 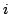 en el estado
en el estado 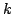 ;
notese que hemos eliminado el subindice
;
notese que hemos eliminado el subindice  en
en 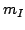 con objeto de simplificar la nomenclatura.
con objeto de simplificar la nomenclatura.
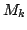 es el número cuántico correspondiente a la componente Z total del momento angular de espín nuclear
y corresponde a la suma de las componentes Z individuales
es el número cuántico correspondiente a la componente Z total del momento angular de espín nuclear
y corresponde a la suma de las componentes Z individuales 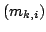 de cada nucleo equivalente
para un estado
de cada nucleo equivalente
para un estado 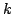 determinado.
Hay
determinado.
Hay 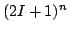 estados de espín nuclear y, por tanto, hay
estados de espín nuclear y, por tanto, hay 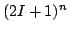 diferentes posibilidades para
diferentes posibilidades para 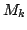 .
Sin embargo, se obtienen solamente
.
Sin embargo, se obtienen solamente 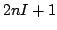 diferentes campos de resonancia
diferentes campos de resonancia 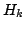 o líneas distintas de RSE.
Esto se debe a que todas las líneas a excepción de la primera y la última están
degeneradas (en la misma posición) de tal
forma que sus intensidades relativas aumentan hacia el centro del espectro.
o líneas distintas de RSE.
Esto se debe a que todas las líneas a excepción de la primera y la última están
degeneradas (en la misma posición) de tal
forma que sus intensidades relativas aumentan hacia el centro del espectro.
Para núcleos con espín 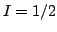 las intensidades relativas vienen dadas por los
coeficientes del binomio
las intensidades relativas vienen dadas por los
coeficientes del binomio 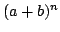 que pueden obtenerse fácilmente a partir del Triángulo
de Pascal (Tabla 2); donde cada número es igual a la suma de los dos que están sobre él, .
En la Tabla 2,
que pueden obtenerse fácilmente a partir del Triángulo
de Pascal (Tabla 2); donde cada número es igual a la suma de los dos que están sobre él, .
En la Tabla 2, 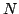 es el número total de líneas y
es el número total de líneas y 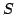 es la suma de cada fila del
Triángulo de Pascal,
es la suma de cada fila del
Triángulo de Pascal, 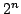 (ó número total de transiciones).
(ó número total de transiciones).
Tabla 2:
Intensidades relativas observadas de para n núcleos con I = 1/2.
| n |
Intensidades relativas |
N |
Multiplete |
S |
| 0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
Singlete |
1 |
| 1 |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
2 |
Doblete |
2 |
| 2 |
|
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
|
|
|
3 |
Triplete |
4 |
| 3 |
|
|
|
|
|
1 |
|
3 |
|
3 |
|
1 |
|
|
|
|
|
4 |
Cuartete |
8 |
| 4 |
|
|
|
|
1 |
|
4 |
|
6 |
|
4 |
|
1 |
|
|
|
|
5 |
Quintete |
16 |
| 5 |
|
|
|
1 |
|
5 |
|
10 |
|
10 |
|
5 |
|
1 |
|
|
|
6 |
Sextete |
32 |
| 6 |
|
|
1 |
|
6 |
|
15 |
|
20 |
|
15 |
|
6 |
|
1 |
|
|
7 |
Septete |
64 |
| 7 |
|
1 |
|
7 |
|
21 |
|
35 |
|
35 |
|
21 |
|
7 |
|
1 |
|
8 |
Octete |
128 |
| 8 |
1 |
|
8 |
|
28 |
|
56 |
|
70 |
|
56 |
|
28 |
|
8 |
|
1 |
9 |
Nonete |
256 |
Triángulo de Pascal
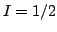
;
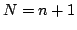
;
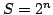
.
El espectro de un radical con dos protones equivalentes (Fig. 3) consta de tres
líneas (
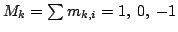 ) y la línea central es de doble intensidad (altura).
El espectro es un triplete de intensidades relativas 1:2:1 y la separación entre dos
líneas consecutivas es la constante de acoplamiento
) y la línea central es de doble intensidad (altura).
El espectro es un triplete de intensidades relativas 1:2:1 y la separación entre dos
líneas consecutivas es la constante de acoplamiento 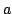 .
Los campos de resonancia obtenidos a partir de la Ec. (6), son:
.
Los campos de resonancia obtenidos a partir de la Ec. (6), son:
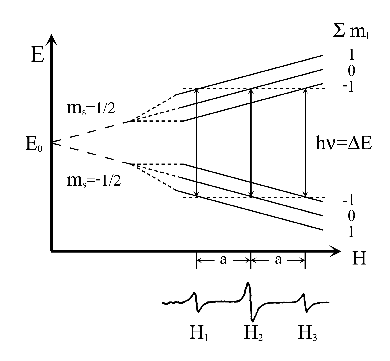
Figura 3:
Niveles de energía de un radical con dos núcleos equivalentes con I = 1/2 y espectro de RSE.
 |
A continuación se incluyen, en orden creciente de dificultad, una serie de espectros de RSE de radicales
que tienen n núcleos (n = 2, 3, 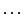 , 8) equivalentes con espín
, 8) equivalentes con espín 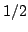 .
.
En todos los casos debes realizar las siguiente operaciones:
- Entra en el simulador pulsando el enlace correspondiente.
- Mide el valor de constante de acoplamiento
(entre los centros de las líneas) en el espectro experimental.
- Utiliza el valor de la constante obtenida para simular el espectro.
- Cuando creas que la simulación es correcta solapa ambos espectros, el simulado y el experimental,
si notas diferencias (no coinciden) refina la constante de acoplamiento y/o varía el ancho pico a pico
(ver Apéndice A).
- Mide las alturas (con el ratón)
de cada una de las líneas y divide el resultado por el
valor de la primera línea (en los radicales [a006] y [a007] es mejor dividir por el valor
de la segunda línea ya que la primera es muy pequeña).
- Observa el número de núcleos equivalentes y las señales que generan.
Compara los resultados obtenidos con los datos de la Tabla 2.
- Imprime el espectro simulado con los parámetros de simulación utilizados.
Cuando termines la simulación cierra la ventana del simulador para volver al tutorial.
Subsecciones



Siguiente: 5.1.1 Radical neutro hidroximetilo
Subir: 5 Espectros de radicales
Anterior: 5 Espectros de radicales
Índice General
Universidad Autónoma de Madrid, Departamento de Química Física Aplicada
![]() y un electrón se muestra en la Fig. 2.
y un electrón se muestra en la Fig. 2.
![]() .
En la parte inferior de la Fig. 2 se ha representado la primera derivada
de la curva de absorción como es usual en Espectroscopia de RSE.
.
En la parte inferior de la Fig. 2 se ha representado la primera derivada
de la curva de absorción como es usual en Espectroscopia de RSE.
![]() núcleos equivalentes (con idéntico entorno químico)
de espín
núcleos equivalentes (con idéntico entorno químico)
de espín ![]() ocasionarán el mismo desdoblamiento hiperfino (igual valor de
ocasionarán el mismo desdoblamiento hiperfino (igual valor de ![]() );
su espectro de RSE estará formado por
);
su espectro de RSE estará formado por ![]() líneas equidistantes a los campos de resonancia:
líneas equidistantes a los campos de resonancia:
![]() las intensidades relativas vienen dadas por los
coeficientes del binomio
las intensidades relativas vienen dadas por los
coeficientes del binomio ![]() que pueden obtenerse fácilmente a partir del Triángulo
de Pascal (Tabla 2); donde cada número es igual a la suma de los dos que están sobre él, .
En la Tabla 2,
que pueden obtenerse fácilmente a partir del Triángulo
de Pascal (Tabla 2); donde cada número es igual a la suma de los dos que están sobre él, .
En la Tabla 2, ![]() es el número total de líneas y
es el número total de líneas y ![]() es la suma de cada fila del
Triángulo de Pascal,
es la suma de cada fila del
Triángulo de Pascal, ![]() (ó número total de transiciones).
(ó número total de transiciones).
![]() ) y la línea central es de doble intensidad (altura).
El espectro es un triplete de intensidades relativas 1:2:1 y la separación entre dos
líneas consecutivas es la constante de acoplamiento
) y la línea central es de doble intensidad (altura).
El espectro es un triplete de intensidades relativas 1:2:1 y la separación entre dos
líneas consecutivas es la constante de acoplamiento ![]() .
Los campos de resonancia obtenidos a partir de la Ec. (6), son:
.
Los campos de resonancia obtenidos a partir de la Ec. (6), son:
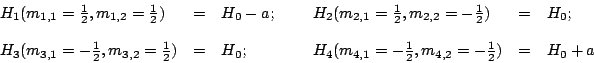

![]() , 8) equivalentes con espín
, 8) equivalentes con espín ![]() .
.