B. Desdoblamientos de segundo orden

El análisis teórico de los desdoblamientos hiperfinos considerados en este tutorial es válido solamente en aquellos casos en que el desdoblamiento Zeeman electrónico $(g\beta H)$ es mucho mayor que el desdoblamiento hiperfino $(a' m_I)$ (ver Ec. (4)). Esta condición se cumple en la mayor parte de los radicales y los términos $-a M_k$ y $-\sum a_j M_{k,j}$ de las Ecs. (6) y (7), que define las posiciones de las líneas con relación al centro del espectro $(H_0)$, se denominan de primer orden.

Para unos pocos radicales, con valores altos de la constante de acoplamiento (o cuando se trabaja a un campo magnético muy bajo) ocurren desdoblamientos adicionales de algunas líneas del espectro dando lugar a los llamados efectos de segundo orden. En el tratamiento teórico de estos efectos, las Ecs. (6) y (7) dejan de ser válidas y debemos añadir un término de desdoblamiento de segundo orden, que es proporcional al cociente $-a^2/2H_0$. Las ecuaciones resultantes que sustituyen, respectivamente, a las Ecs. (6) y (7) son:

$$H_k = H_0 - a M_k - \frac{a^2}{2 H_0} \left [ I_k (I_k + 1) - M_k^2 \right ]$$ (11)

y

$$H_k = H_0 - \sum_{j=1}^{r} \left \{ a_j M_{k,j} - \frac{a^... ...} \left [ I_{k,j} (I_{k,j} + 1) - M_{k,j}^2 \right ] \right \}$$ (12)

donde $I_k$ o $I_{k,j}$ es el número cuántico correspondiente al modulo del momento angular de espín nuclear del grupo de nucleos equivalente $j$ en el estado $k$ y $M_k = \sum_{i=1}^{n} m_{k,i}$ o $M_{k,j} = \sum_{i=1}^{n} m_{k,j,i}$ son los números cuánticos correspondiente a la proyección del momento angular de espín nuclear del grupo de nucleos equivalente $j$ en el estado $k$.

El desdoblamiento de segundo orden puede resolverse cuando $-a^2/2H_0$ es comparable con el valor DHpp de las líneas del espectro. De este modo, para un campo de 340 mT y un valor de DHpp=0.01mT, el valor de la constante ha de ser mayor de 2.6 mT.

Un ejemplo de espectro de segundo orden es el del radical neutro $\cdot CF_3$ con tres núcleos de fluor equivalentes y una constante de acoplamiento elevada (14.45 mT). El espectro de este radical no da cuatro líneas como en el caso del radical $\cdot CH_3$, sino que su espectro realizado a alta resolución consta de seis líneas debido a los desdoblamientos de segundo orden¹.

Cuando la muestra se enriquece con $^{13}C$, se observa además su acoplamiento con el electrón desapareado con una constante de 27.16 mT. En la Fig. 42 se muestra el espectro del radical $\cdot ^{13}CF_3$ simulado como primer y como segundo orden. Los estado de espín posibles del $^{13}C$ son dos $I = 1/2; \ M = +1/2$ y $I = 1/2: \ M = -1/2$. Más complicados son los estados de espín de los tres fluor equivalentes. Estos estados se presentan en la Tabla 5.

Tabla 5: Estados de espín nuclear para tres fluor equivalentes.

Estado	$m_{k,i}$			$M_k^a$	$I_k^b$
k	$F_1$	$F_2$	$F_3$
1	$\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$	$\ \frac{3}{2}$	$\ \frac{3}{2}$
2	$\frac{1}{2}$	$\frac{1}{2}$	$-\frac{1}{2}$	$\frac{1}{2}$	$\ \frac{3}{2}$
3	$\frac{1}{2}$	$-\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$
4	$-\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$
5	$-\frac{1}{2}$	$-\frac{1}{2}$	$\frac{1}{2}$	$-\frac{1}{2}$	$\ \frac{3}{2}$
6	$-\frac{1}{2}$	$\frac{1}{2}$	$-\frac{1}{2}$	$-\frac{1}{2}$	$\frac{1}{2}$
7	$\frac{1}{2}$	$-\frac{1}{2}$	$-\frac{1}{2}$	$-\frac{1}{2}$	$\frac{1}{2}$
8	$-\frac{1}{2}$	$-\frac{1}{2}$	$-\frac{1}{2}$	$-\frac{3}{2}$	$\ \frac{3}{2}$

$^a$ $M_k =$ $\sum m_{k,i}$.
$^b$ En algunos casos la asignación del número cuántico $I_k$ es arbitraria, por ejemplo el segundo estado marcado con $I_2 = 3/2$ y el tercero con $I_3 = 1/2$ podrían intercambiarse.

Aplicando la Ec. (12) a la molécula $\cdot ^{13}CF_3$ se puede obtener el espectro simulado de EPR de segundo orden. En la Tabla 6 mostramos las diferentes señales de primer y segundo orden que nos da el espectro simulado de EPR.

Tabla 6: Desplazamiento respecto a $H_0$ de las 12 señales del espectro del radical $\cdot ^{13}CF_3$

C		F		Primer orden			Segundo orden			Intensidad
$I_{k}$	$M_{k,j}^b$	$I_{k}$	$M_{k,j}^b$	$H_r -H_0$, Ec. (7)	Señal$^a$ (mT)		Térm. adicionales, Ec. (12)	Señal$^a$ (mT)		relativa
$\frac{1}{2}$	$\frac{1}{2}$	$\ \frac{3}{2}$	$\ \frac{3}{2}$	$-\frac{1}{2} a_C - \frac{3}{2} a_F$	$a_1$	-35.25	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{3}{2}\frac{a_F^2}{2H_0}$	$b_1$	-36.26	1
$\frac{1}{2}$	$\frac{1}{2}$	$\ \frac{3}{2}$	$\frac{1}{2}$	$-\frac{1}{2} a_C - \frac{1}{2} a_F$	$a_2$	-20.80	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{7}{2}\frac{a_F^2}{2H_0}$	$b_2$	-22.42	1
$\frac{1}{2}$	$\frac{1}{2}$	$\ \frac{3}{2}$	$-\frac{1}{2}$	$-\frac{1}{2} a_C + \frac{1}{2} a_F$	$a_4$	-6.36	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{7}{2}\frac{a_F^2}{2H_0}$	$b_5$	-7.97	1
$\frac{1}{2}$	$\frac{1}{2}$	$\ \frac{3}{2}$	$-\frac{3}{2}$	$-\frac{1}{2} a_C + \frac{3}{2} a_F$	$a_6$	8.09	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{3}{2}\frac{a_F^2}{2H_0}$	$b_9$	7.09	1
$\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$	$-\frac{1}{2} a_C - \frac{1}{2} a_F$	$a_2$	-20.80	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{1}{2}\frac{a_F^2}{2H_0}$	$b_3$	-21.50	2
$\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$	$-\frac{1}{2}$	$-\frac{1}{2} a_C + \frac{1}{2} a_F$	$a_4$	-6.36	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{1}{2}\frac{a_F^2}{2H_0}$	$b_6$	-7.05	2
$\frac{1}{2}$	$-\frac{1}{2}$	$\ \frac{3}{2}$	$\ \frac{3}{2}$	$+\frac{1}{2} a_C - \frac{3}{2} a_F$	$a_3$	-8.09	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{3}{2}\frac{a_F^2}{2H_0}$	$b_{4}$	-9.10	1
$\frac{1}{2}$	$-\frac{1}{2}$	$\ \frac{3}{2}$	$\frac{1}{2}$	$+\frac{1}{2} a_C - \frac{1}{2} a_F$	$a_5$	+6.36	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{7}{2}\frac{a_F^2}{2H_0}$	b$_{7}$	4.74	1
$\frac{1}{2}$	$-\frac{1}{2}$	$\ \frac{3}{2}$	$-\frac{1}{2}$	$+\frac{1}{2} a_C + \frac{1}{2} a_F$	$a_7$	+20.80	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{7}{2}\frac{a_F^2}{2H_0}$	$b_{10}$	19.19	1
$\frac{1}{2}$	$-\frac{1}{2}$	$\ \frac{3}{2}$	$-\frac{3}{2}$	$+\frac{1}{2} a_C + \frac{3}{2} a_F$	$a_8$	+35.25	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{3}{2}\frac{a_F^2}{2H_0}$	$b_{12}$	34.25	1
$\frac{1}{2}$	$-\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$	$+\frac{1}{2} a_C - \frac{1}{2} a_F$	$a_5$	+6.36	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{1}{2}\frac{a_F^2}{2H_0}$	b$_8$	5.66	2
$\frac{1}{2}$	$-\frac{1}{2}$	$\frac{1}{2}$	$-\frac{1}{2}$	$+\frac{1}{2} a_C + \frac{1}{2} a_F$	$a_7$	+20.80	$- \frac{1}{2} \frac{a_C^2}{2H_0}- \frac{1}{2}\frac{a_F^2}{2H_0}$	$b_{11}$	20.11	2

$^a$Con las constantes hiperfinas $a_C = 27.16$ mT y $a_F = 14.45$ mT en un campo magnético externo $H_0 = 340$ mT.
$^b$ $M_{k,j} = \sum m_{k,j,i}$.

La Tabla 7 compara número total de líneas y sus intensidades relativas para núcleos con $I=1/2$ considerando que el espectro es de primer orden y su diferencia con el de segundo orden.

Tabla 7: Intensidades observadas para n núcleos con $I=1/2$.

n	Intensidades relativas$^a$	N	Intensidades relativas$^b$	N	S$^c$
1	1 : 1	2	1 : 1	2	2
2	1 : 2: 1	3	1: 1, 1: 1	4	4
3	1: 3: 3: 1	4	1: 1, 2: 1, 2: 1	6	8
4	1:4:6:4:1	5	1: 1,3: 1,3,2: 1,3: 1	9	16

$^a$Espectro de primer orden.
$^b$Espectro de segundo orden.
$^c$ $S=2^n$.

Al pasar del modelo de primer orden al de segundo orden se observa lo siguiente sobre el espectro:

1. Todas las líneas a excepción de la más externas se desdoblan.
2. Todas las líneas excepto las centrales (señaladas en negrita en la Tabla 7) se desplazan ligeramente a un campo magnético menor.
3. La suma total de las intensidades de todas las líneas de cada uno de los multipletes $(S)$ es, lógicamente, la misma en los espectros de primer orden y de segundo orden.
4. La longitud total del espectro permanece constante al pasar de la simulación de primer a la de segundo orden. En la Tabla 6 se puede comprobar que la longitud del espectro del radical $\cdot ^{13}CF_3$ es en ambos caso 70.5 mT.

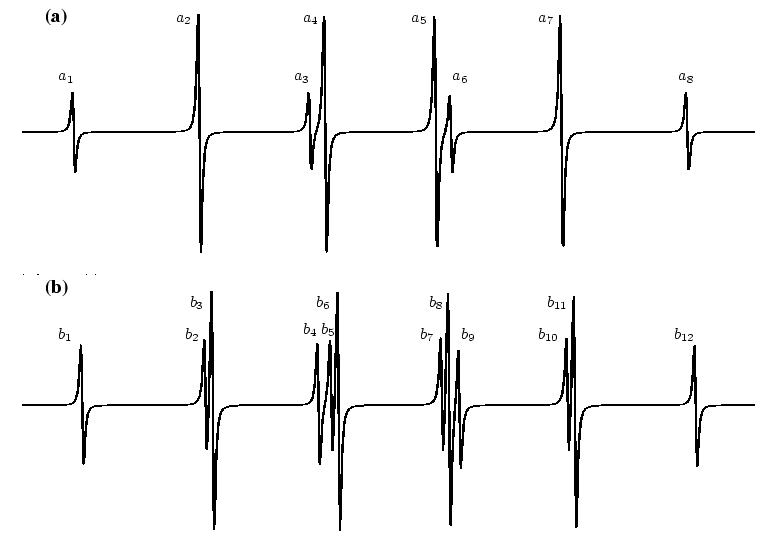
En la Fig. 42 se muestra la simulación del radical $\cdot ^{13}CF_3$ según un desdoblamiento de primer orden (a) o de segundo orden (b). Esta última simulación es la más parecida al espectro experimental.

Figura 42: Simulación del radical $\cdot ^{13}CF_3$ según un desdoblamiento de primer orden (a) o de segundo orden (b).

Es importante recordar que los espectros y las simulaciones presentadas y realizadas en este tutorial corresponde exclusivamente a desdoblamientos de primer orden.